There is often the requirement to evaluate descriptive statistics for data within the organization or for health care information. Every year the National Cancer Institute
There is often the requirement to evaluate descriptive statistics for data within the organization or for health care information. Every year the National Cancer Institute collects and publishes data based on patient demographics. Understanding differences between the groups based upon the collected data often informs health care professionals towards research, treatment options, or patient education.
Using the data on the “National Cancer Institute Data” Excel spreadsheet, calculate the descriptive statistics indicated below for each of the Race/Ethnicity groups. Refer to your textbook and the Topic Materials, as needed, for assistance in with creating Excel formulas.
Provide the following descriptive statistics:
- Measures of Central Tendency: Mean, Median, and Mode
- Measures of Variation: Variance, Standard Deviation, and Range (a formula is not needed for Range).
- Once the data is calculated, provide a 150-250 word analysis of the descriptive statistics on the spreadsheet. This should include differences and health outcomes between groups.
APA style is not required, but solid academic writing is expected.
This assignment uses a rubric. Please review the rubric prior to beginning the assignment to become familiar with the expectations for successful completion.
You are not required to submit this assignment to LopesWrite.
Expert Answer and Explanation
Alternative Expert Answer and Explanation
Measures of Central Tendency: Mean, Median, and Mode
This paper will elaborate on the descriptive statistical analysis for lung and bronchus cancer for the different racial groups as contained in the National Cancer Institute (2018). The data compiled was from the years 2000 to 2015.
Mean
Mean, also known as average, is the total summation of the values given divided by the number of items in a data set (Grove & Gray, 2018). The following is a mean for the different racial groups:
Mean = Σ/n. where Σ is the total sum of the rate per 100,000, and n is the number of years (16 years).
American Indian / Alaska Native (includes Hispanic)
Mean = 692.4/16 = 43.275
Asian / Pacific Islander (includes Hispanic)
Mean = 616.2/16 = 38.5125
Black (includes Hispanic)
Mean = 1121.1/16 = 70.06875
Hispanic (any race)
Mean = 503.9/16= 31.49375
White (includes Hispanic)
Mean = 1003.6/16=62.725
Median
Median is defined as the middle number in a data set (Grove & Gray, 2018). Given that the data set used by this paper contains an even number of items, one can get the median by calculating the average of the two middle numbers. The median for the following racial groups is calculated as follows
American Indian / Alaska Native (includes Hispanic)
Median = (43.1+44.6)/2 = 43.85
Asian / Pacific Islander (includes Hispanic)
Median = (38.8+39)/2 = 38.9
Black (includes Hispanic)
Median = (71.2+71.6)/2 =71.4
Hispanic (any race)
Median = (32+32.2)/2 =32.1
White (includes Hispanic)
Median = (63.9+65.2)/2 = 64.55
Mode
Mode is defined as the most repeated number in a data set. In case a modal value can’t be established, one is supposed to group the data values, and using the following formula; the modal value for the group can be identified.
Mode = L + (fm − fm-1) / ((fm − fm-1) + (fm − fm+1)) × W
where:
- L is the lower-class boundary of the modal group
- fmis the frequency of the modal group
- fm-1is the frequency of the group before the modal group
- fm+1is the frequency of the group after the modal group
- w is the group width
American Indian / Alaska Native (includes Hispanic)
Data Groups 31-40 frequency = 6, 41-50 frequency = 9, 51-60 frequency = 1
The modal estimation for this population group is
Mode = 41+ (9 − 6) / ((9 − 6) + (9 − 1)) × 10 = 41 +3/11 x 10 = 43.73
Ans = 43.73
Asian / Pacific Islander (includes Hispanic)
The mode for this population group is 36,6
Black (includes Hispanic)
Data Groups 55-60 frequency = 2, 61-65 frequency =3, 66-70 frequency =2, 71-75 frequency =6, 76–80 frequency = 3
The modal estimation for this population group is
Mode = 71+ (6 − 2) / ((6 − 2) + (6 − 3)) × 5 = 71 +4/7 x 10 = 76.71
Ans = 76.71
Hispanic (any race)
The mode for this population group is 34.1
White (includes Hispanic)
The mode for this population group is 65.8
Measures of Variation:
Variance
Variance is the measurement of how numbers are distributed in a given data set. The following is a formula used to calculate variance;
Σ (Xi – μ) 2 / n.
Where:
Σ is summation of the items
n is the total number of items in the data set.
Xi is the individual figures in the data set,
μ is the mean for that data set,
The following is the variance for the given racial groups
American Indian / Alaska Native (includes Hispanic)
μ = 43.275
| Xi | (μ – Xi)2 |
| 32 | 127.125625 |
| 36.6 | 44.555625 |
| 38.7 | 20.930625 |
| 39.6 | 13.505625 |
| 39.9 | 11.390625 |
| 40.1 | 10.080625 |
| 42.4 | 0.765625 |
| 43.1 | 0.030625 |
| 44.6 | 1.755625 |
| 45 | 2.975625 |
| 45.7 | 5.880625 |
| 46.4 | 9.765625 |
| 47.9 | 21.390625 |
| 48.7 | 29.430625 |
| 50 | 45.225625 |
| 51.7 | 70.980625 |
| Σ =415.79 |
Variance = 415.79/16 = 25.986875
Asian / Pacific Islander (includes Hispanic)
μ = 38.5125
| Xi | (μ – Xi)2 |
| 34 | 20.36265625 |
| 34.4 | 16.91265625 |
| 36.6 | 3.65765625 |
| 36.6 | 3.65765625 |
| 36.7 | 3.28515625 |
| 37 | 2.28765625 |
| 38.5 | 0.00015625 |
| 38.8 | 0.08265625 |
| 39 | 0.23765625 |
| 39.8 | 1.65765625 |
| 40.2 | 2.84765625 |
| 40.4 | 3.56265625 |
| 40.5 | 3.95015625 |
| 40.9 | 5.70015625 |
| 41 | 6.18765625 |
| 41.8 | 10.80765625 |
| Σ =85.1975 |
Variance = 85.1975/16 = 5.32484375
Black (includes Hispanic)
μ = 38.5125
| Xi | (μ – Xi)2 |
| 57.4 | 160.4972266 |
| 60.5 | 91.56097656 |
| 61.3 | 76.89097656 |
| 64.1 | 35.62597656 |
| 64.3 | 33.27847656 |
| 67.8 | 5.147226562 |
| 70.8 | 0.534726563 |
| 71.2 | 1.279726563 |
| 71.6 | 2.344726563 |
| 73.4 | 11.09722656 |
| 73.7 | 13.18597656 |
| 75.1 | 25.31347656 |
| 75.8 | 32.84722656 |
| 77.3 | 52.29097656 |
| 77.8 | 59.77222656 |
| 79 | 79.76722656 |
| Σ = 681.4344 |
Variance = 681.4344/16 = 42.58965
Hispanic (any race)
μ = 31.49375
| Xi | (μ – Xi)2 |
| 26 | 30.18128906 |
| 26.8 | 22.03128906 |
| 28.2 | 10.84878906 |
| 28.8 | 7.256289062 |
| 29.4 | 4.383789063 |
| 30.3 | 1.425039062 |
| 31.8 | 0.093789063 |
| 32 | 0.256289063 |
| 32.2 | 0.498789063 |
| 32.7 | 1.455039063 |
| 33.8 | 5.318789062 |
| 34.1 | 6.792539063 |
| 34.1 | 6.792539063 |
| 34.2 | 7.323789063 |
| 34.5 | 9.037539063 |
| 35 | 12.29378906 |
| Σ =125.989375
|
Variance = 125.989375/16 = 7.8743359375
White (includes Hispanic)
μ = 38.5125
| Xi | (μ – Xi)2 |
| 53.2 | 90.725625 |
| 55.4 | 53.655625 |
| 56.3 | 41.280625 |
| 57.5 | 27.300625 |
| 58.5 | 17.850625 |
| 60.4 | 5.405625 |
| 63.1 | 0.140625 |
| 63.9 | 1.380625 |
| 65.2 | 6.125625 |
| 65.8 | 9.455625 |
| 65.8 | 9.455625 |
| 65.9 | 10.080625 |
| 67.1 | 19.140625 |
| 68 | 27.825625 |
| 68.7 | 35.700625 |
| 68.8 | 36.905625 |
| Σ =392.43 |
Variance = 392.43/16 = 24.526875
Standard Deviation
Standard deviation (SD) is calculated by finding the square root of variance; the following is the SD for each of the racial groups;
American Indian / Alaska Native (includes Hispanic)
SD = √25.986875 = 5.097732
Asian / Pacific Islander (includes Hispanic)
SD = √5.32484375 = 2.307562
Black (includes Hispanic)
SD = √42.58965 = 6.526075
Hispanic (any race)
SD = √7.8743359375 =2.8061247
White (includes Hispanic)
SD = √24.526875 = 4.9524615
Range.
The following is the range for the given racial groups
American Indian / Alaska Native (includes Hispanic)
Range = 51.7- 32 = 19.7
Asian / Pacific Islander (includes Hispanic)
Range = 41.8- 34 = 7.8
Black (includes Hispanic)
Range = 79- 57.4 = 22.4
Hispanic (any race)
Range = 35- 26 = 9
White (includes Hispanic)
Range = 68.8- 53.2 = 15.6
Summary of the descriptive statistics
The following is a summary of the results obtained from the statistical analysis of lung and bronchus cancer cases in the US for the periods between 2000 and 2015. The statistical analysis which was conducted using descriptive statistics included two major components i.e., measures of central tendency (mean mode and median) and measures of variance (standard deviation, variance and range).
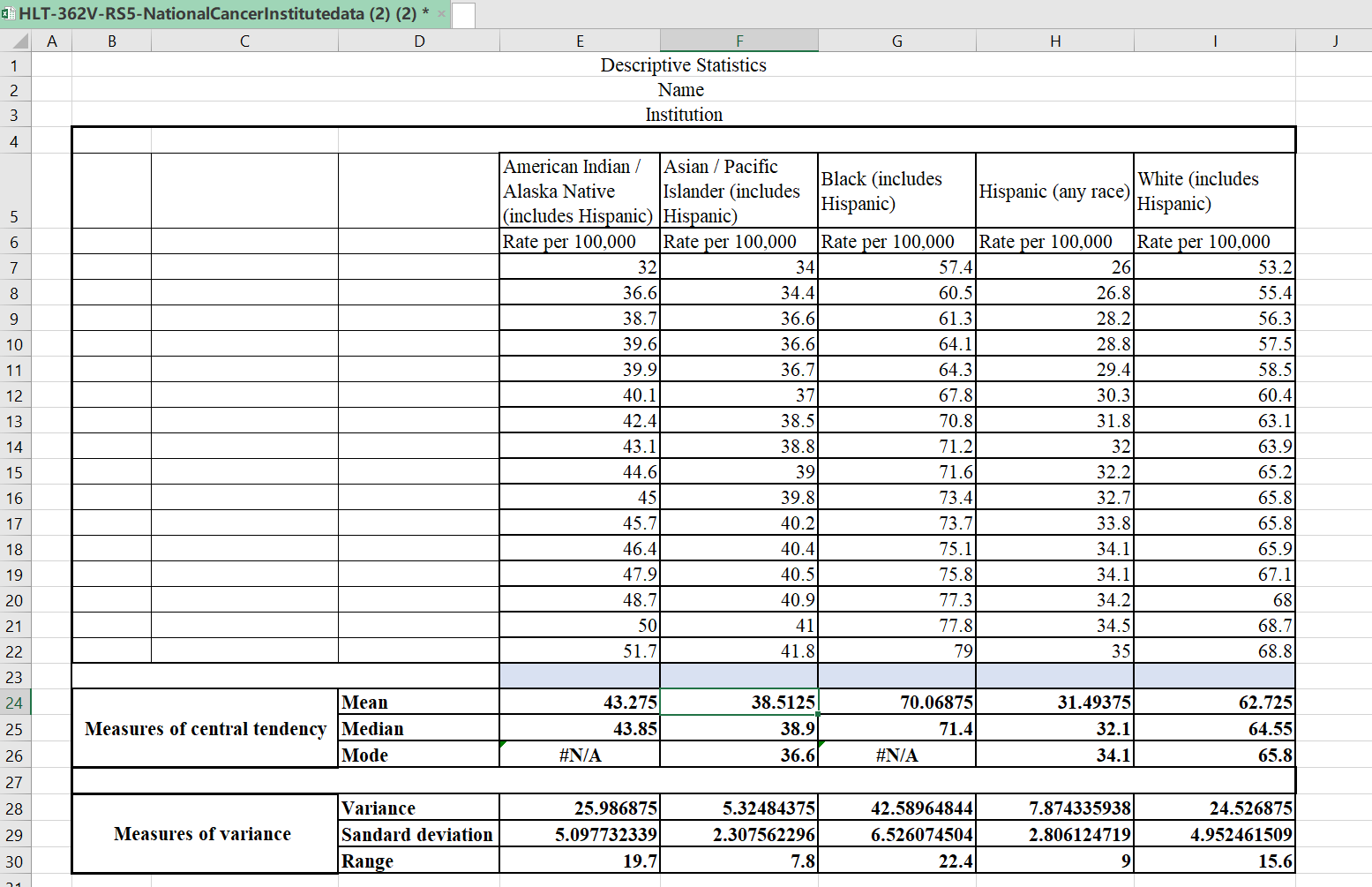
From the analysis it was found out that the African American population had the highest mean in terms of the number of lung and bronchus cancer at 70.06875. This was followed by non-Hispanic Whites who had the second highest mean of 62.725. The Hispanic population had the least mean of 31.49375.
With regards to the median rate for lung and bronchus cancer, it was noted that the American Indian / Alaska Native (includes Hispanic) had a median of 43.85, Asian / Pacific Islander (includes Hispanic) had a median of 38.9. For Blacks (includes Hispanic), the median was 71.4, while the Hispanic (any race) had a median of 32.1. Lastly, the Whites (includes Hispanic) had a median of 64.55.
from the analysis of variance, it was established that, Blacks had the highest level of variance at 42.58965 with the second highest being American Indian / Alaska Native (includes Hispanic) with a variance of 25.986875. The Asian / Pacific Islander (includes Hispanic) had the least variance at 5.32484375. The widest range was noted from Black population at 22.4, with the e Asian / Pacific Islanders recording the smallest range of 7.8.
Other Solved Questions:
SOLVED! How would your communication and interview
SOLVED! Describe the difference between a nursing practice
SOLVED! How do you think evidence from nursing journals
SOLVED! Discuss how elimination complexities can affect
SOLVED! Case C 38-year-old Native American pregnant
ANSWERED! In a 1,000–1,250 word essay, summarize two
[ANSWERED] Students will develop a 1,250-1,500 word paper that includes
[ANSWERED] Post a description of the national healthcare
ANSWERED!! Explain how you would inform this nurse
ANSWERED!! In a 4- to 5-page project proposal written to the
ANSWERED!! A 15-year-old male reports dull pain in both
ANSWERED!! Should government continue to take an
[ANSWERED] Mrs. Adams a 68-year-old widow who was
[ANSWERED] Compare and contrast the various ways you can
ANSWERED! Provide a summary of your learning style
FAQs
Descriptive statistics for data analysis
Descriptive statistics is a branch of statistics that involves the collection, organization, analysis, interpretation, and presentation of data. It provides a way to summarize and describe the main features of a dataset. The main objective of descriptive statistics is to provide a clear and concise summary of data in order to make it more understandable and usable for decision making.
There are several key measures used in descriptive statistics to analyze a dataset. Some of the most commonly used measures are:
- Measures of central tendency: These measures describe the typical or central value of a dataset. The three most common measures of central tendency are the mean, median, and mode.
- Measures of dispersion: These measures describe the spread or variability of the data. The most commonly used measures of dispersion are the range, variance, and standard deviation.
- Measures of shape: These measures describe the shape of the distribution of the data. The most commonly used measures of shape are skewness and kurtosis.
- Frequency distribution: A frequency distribution is a table that shows how often each value or range of values occurs in a dataset.
- Graphical representations: Graphical representations such as histograms, box plots, and scatter plots are commonly used to visualize and summarize data.
Descriptive statistics can be used in a variety of fields, including business, economics, psychology, medicine, and many others. It is a valuable tool for analyzing and interpreting data, as it helps researchers and decision makers to better understand the characteristics of a dataset and to make more informed decisions based on the data.
